1.概述
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,由于算法的简单和高效,在实际中应用非常广泛。
2.配置参数
拖拽一个数据集和一个逻辑回归节点到画布,连接数据集和逻辑回归节点。
添加逻辑回归模型到实验后,可通过右侧的“配置项目”页面,对模型进行设置。
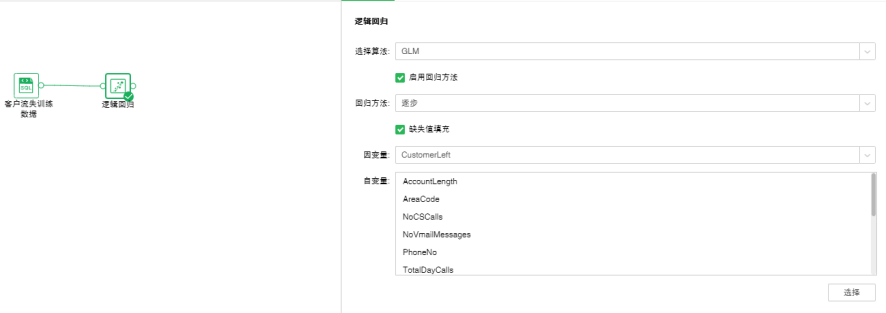
逻辑回归有两种算法:GLM,GLMNET,默认是GLM。
2.1GLM
广义线性模型(GLM),这种模型是把自变量的线性预测函数当作因变量的估计值。常用于逻辑回归中。
【启用回归方法】控制是否使用回归方法。默认选中。
【回归方法】包含逐步、向前、向后。默认选中逐步。
•逐步:就是分步构建方程式。初始模型是尽可能简单的模型,其方程式中不含任何输入字段。在每个步骤中,对尚未添加到模型的输入字段进行评估,如果其中的最佳输入字段能够显著增加模型预测能力,那么将该字段添加到模型中。此外,还会重新评估当前包含在模型中的输入字段,以确定能否在不对模型功能造成重大减损的情况下删除其中任何字段。如果可以,则会将其删除。然后重复此过程,添加或删除其他字段。当无法再添加任何字段来改进模型、且无法再删除任何字段而不对模型功能造成减损时,最终模型便已生成。
•向后:与分步构建模型的逐步法类似。但是,采用这种方法时,初始模型包含作为预测变量的所有输入字段,只能从模型中删除字段。对模型影响较小的输入字段将被逐一删除,直到无法再删除任何字段而不对模型功能造成重大损害,从而生成最终模型。
•向前:向前与向后是相反的回归方法。采用这种方法,初始模型是最简单的模型,不包含任何输入字段,只能向模型中添加字段。每个步骤会对尚未纳入到模型中的输入字段进行检验,看它们对模型的改进起多大作用,然后将其中的最佳字段添加到模型中。当无法再添加任何字段、或最佳备选字段无法对模型产生足够的改进时,最终模型便已生成。
【缺失值填充】用自变量列平均值填充此列的空值。默认是填充的。
【因变量】从下拉列表中选出需要作为因变量的字段。任何一个系统(或模型)都是由各种变量构成的,当我们分析这些系统(或模型)时,可以选择研究其中一些变量对另一些变量的影响,那么我们选择的这些变量就称为自变量,而被影响的量就被称为因变量。
【自变量】从选择列对话框中选出需要作为自变量的字段。
2.2GLMNET
GLMNET使用Lasso 、 Elastic-Net 等正则化方式来实现逻辑回归。
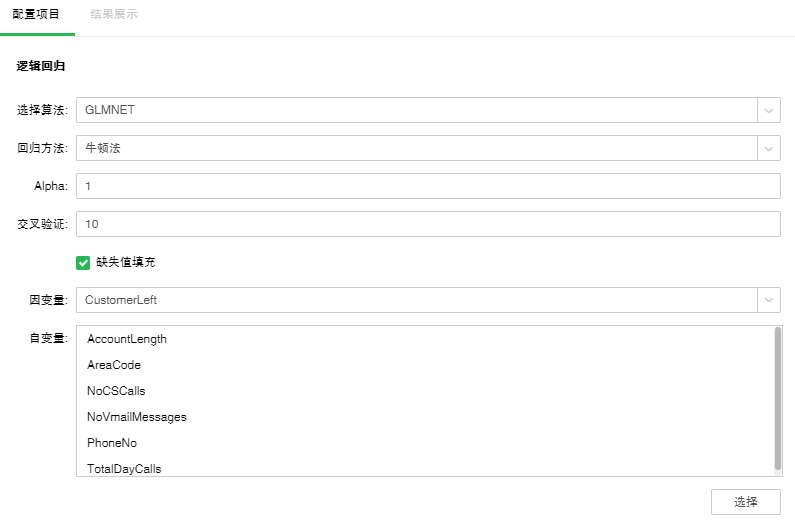
【回归方法】包含牛顿法、拟牛顿法。默认选中牛顿法。
•牛顿法:数值优化的一种方法,利用函数在当前点的一阶导数,以及二阶导数,寻找搜寻方向。
•拟牛顿法: 牛顿法的变形,用近似矩阵替代牛顿法中的海森矩阵。
【Alpha】Elastic-Net混合参数。范围是0到1。等于1时,惩罚项采用L1范数;等于0时,惩罚项采用L2范数。默认值为1。
【交叉验证】通过交叉验证可以得到最优的方程。默认值是10。
3.查看模型结果
逻辑回归模型第一次运行成功后,会自动切换到“结果展示”页面,查看实验模型的结果,再次运行时则不会自动切换,可以手工切换至结果展示页面。
•模型系数
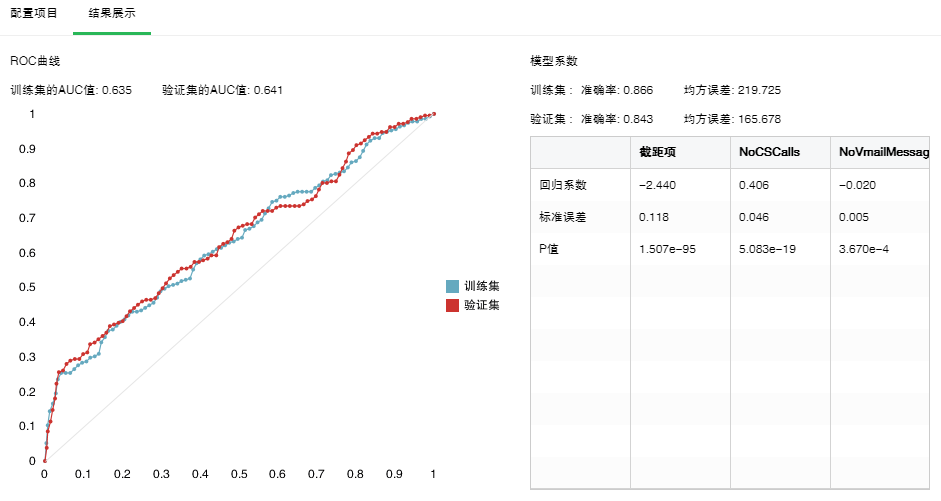
GLM算法通过模型系数可以得到逻辑回归方程的系数,包括截距项,各自变量的系数以及它们的P值,标准误差。还可以看到模型训练后的准确率和均方误差。如果做了数据分区,还能看到基于验证集的模型准确率和均方误差。以下是算法为GLM时的结果。如果系数为0,结果就不会显示在模型系数表格里。
•ROC曲线
绘制ROC曲线计算AUC值,AUC值越大模型分类效果越好。如果做了数据分区还可以比较验证集的AUC值。