|
<< Click to Display Table of Contents >> LDA线性分类 |
|
|
<< Click to Display Table of Contents >> LDA线性分类 |
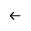  
|
❖LDA线性分类
LDA 线性分类(Linear Discriminant Analysis, LDA) 的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空
间维数的效果。投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。 LDA 线性分类通
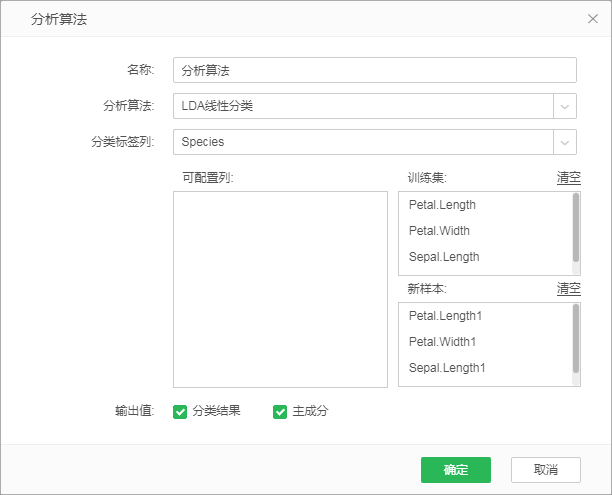
过分类标签列和训练集数据列,调用lda 函数得到lda 模型,根据模型对新样本数据进行预测分类。
【分类标签列】样本数据标签列,每个样本数据都有对应的标签值。
【训练集】样本数据列。从左侧的可配置列中选择需要作为训练集的字段直接拖入到训练集框中。
【新样本】新样本数据列。从左侧的可配置列中选择需要作为新样本的字段直接拖入到新样本框中。新样本的数据行数可以和训练集数据行数不一致。
【输出值】【分类结果】新样本数据的预测标签值。
【输出值】【主成分】对分类的特征做主成分分析,取最重要的两个成分。
•举例说明
已知三种花的样本数据,根据样本数据(花瓣和萼片的长宽值)建立合适的线性分类函数,根据线性分类函数对新样本进行预测分类。
在图表上创建LDA 线性分类分析,如图:
分类结果如图: