|
<< Click to Display Table of Contents >> 算法 |
|
|
<< Click to Display Table of Contents >> 算法 |
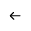  
|
建模包含逻辑回归、决策树、K-Means聚类、关联规则、时序分析。
❖逻辑回归
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,由于算法的简单和高效,在实际中应用非常广泛。
拖拽一个数据集和一个逻辑回归节点到编辑区,连接数据集和逻辑回归节点。选中逻辑回归节点设置及展示区包含两个页面:配置项目、结果展示。
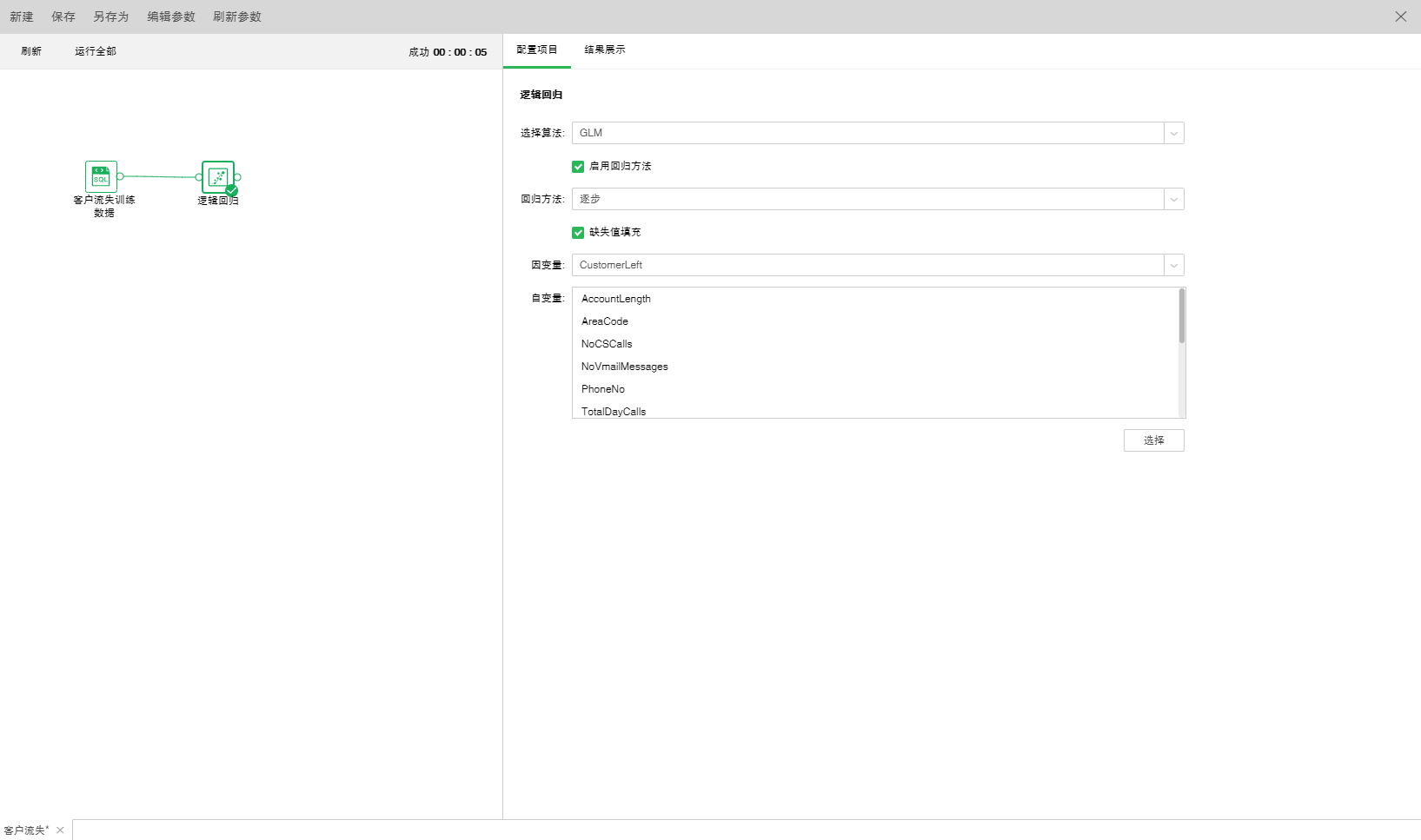
o配置项目
逻辑回归有两种算法:GLM,GLMNET,默认是GLM。
GLM:
广义线性模型(GLM),这种模型是把自变量的线性预测函数当作因变量的估计值。常用于逻辑回归中。
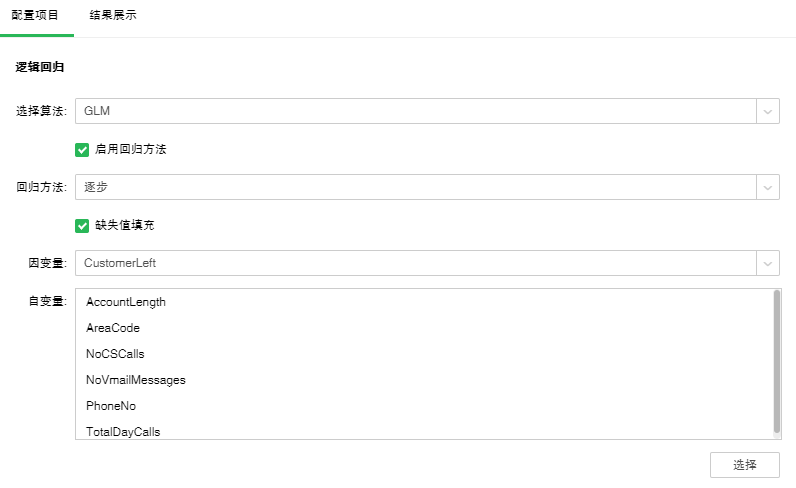
【启用回归方法】控制是否使用回归方法。默认选中。
【回归方法】包含逐步、向前、向后。默认选中逐步。
逐步:就是分步构建方程式。初始模型是尽可能简单的模型,其方程式中不含任何输入字段。在每个步骤中,对尚未添加到模型的输入字段进行评估,如果其中的最佳输入字段能够显著增加模型预测能力,那么将该字段添加到模型中。此外,还会重新评估当前包含在模型中的输入字段,以确定能否在不对模型功能造成重大减损的情况下删除其中任何字段。如果可以,则会将其删除。然后重复此过程,添加或删除其他字段。当无法再添加任何字段来改进模型、且无法再删除任何字段而不对模型功能造成减损时,最终模型便已生成。
向后:与分步构建模型的逐步法类似。但是,采用这种方法时,初始模型包含作为预测变量的所有输入字段,只能从模型中删除字段。对模型影响较小的输入字段将被逐一删除,直到无法再删除任何字段而不对模型功能造成重大损害,从而生成最终模型。
向前:向前与向后是相反的回归方法。采用这种方法,初始模型是最简单的模型,不包含任何输入字段,只能向模型中添加字段。每个步骤会对尚未纳入到模型中的输入字段进行检验,看它们对模型的改进起多大作用,然后将其中的最佳字段添加到模型中。当无法再添加任何字段、或最佳备选字段无法对模型产生足够的改进时,最终模型便已生成。
【缺失值填充】用自变量列平均值填充此列的空值。默认是填充的。
【因变量】从下拉列表中选出需要作为因变量的字段。任何一个系统(或模型)都是由各种变量构成的,当我们分析这些系统(或模型)时,可以选择研究其中一些变量对另一些变量的影响,那么我们选择的这些变量就称为自变量,而被影响的量就被称为因变量。
【自变量】从选择列对话框中选出需要作为自变量的字段。
GLMNET:
GLMNET使用Lasso 、 Elastic-Net 等正则化方式来实现逻辑回归。
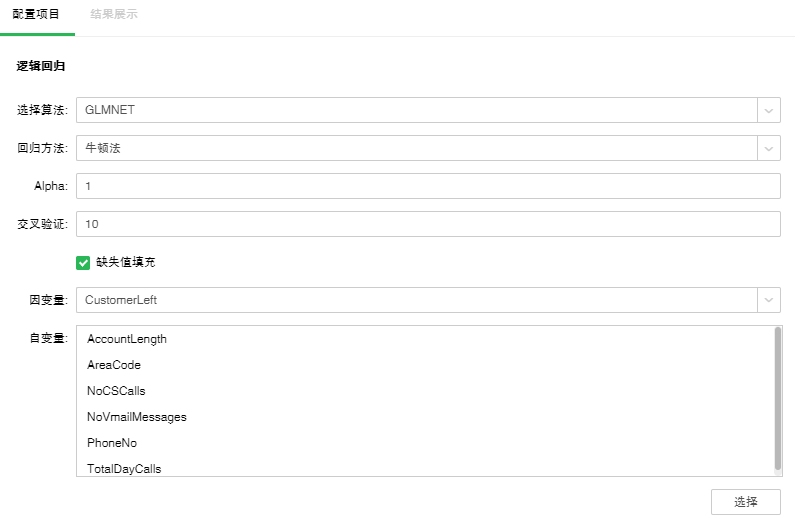
【回归方法】包含牛顿法、拟牛顿法。默认选中牛顿法。
牛顿法:数值优化的一种方法,利用函数在当前点的一阶导数,以及二阶导数,寻找搜寻方向。
拟牛顿法: 牛顿法的变形,用近似矩阵替代牛顿法中的海森矩阵。
【Alpha】Elastic-Net混合参数。范围是0到1。等于1时,惩罚项采用L1范数;等于0时,惩罚项采用L2范数。默认值为1。
【交叉验证】通过交叉验证可以得到最优的方程。默认值是10。
o结果展示
1. 模型系数
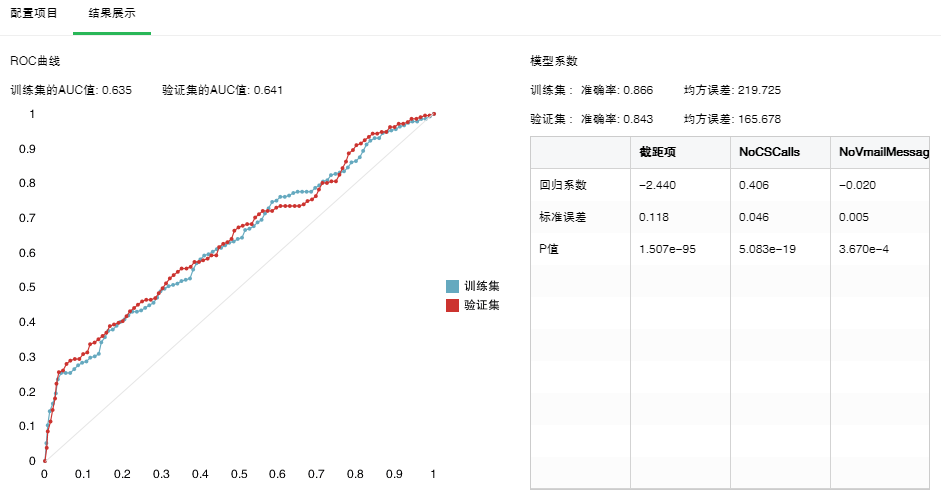
GLM算法通过模型系数可以得到逻辑回归方程的系数,包括截距项,各自变量的系数以及它们的P值,标准误差。还可以看到模型训练后的准确率和均方误差。如果做了数据分区还能看到基于验证集的模型准确率和均方误差。以下是GLM是算法的结果。如果系数为0,结果就不会显示在模型系数表格里。
2. ROC曲线
绘制ROC曲线计算AUC值,AUC值越大模型分类效果越好。如果做了数据分区还可以比较验证集的AUC值。
❖决策树
决策树是一种用于对实例进行分类的树形结构。决策树由节点(node)和有向边(directed edge)组成。节点的类型有两种:内部节点和叶子节点。其中,内部节点表示一个特征或属性的测试条件(用于分开具有不同特性的记录),叶子节点表示一个分类。
一旦我们构造了一个决策树模型,以它为基础来进行分类将是非常容易的。具体做法是,从根节点开始,用实例的某一特征进行测试,根据测试结构将实例分配到其子节点(也就是选择适当的分支);沿着该分支可能达到叶子节点或者到达另一个内部节点时,那么就使用新的测试条件递归执行下去,直到抵达一个叶子节点。当到达叶子节点时,我们便得到了最终的分类结果。
拖拽一个数据集和一个决策树节点到编辑区,连接数据集和决策树节点。选中决策树节点设置及展示区包含两个页面:配置项目、结果展示。
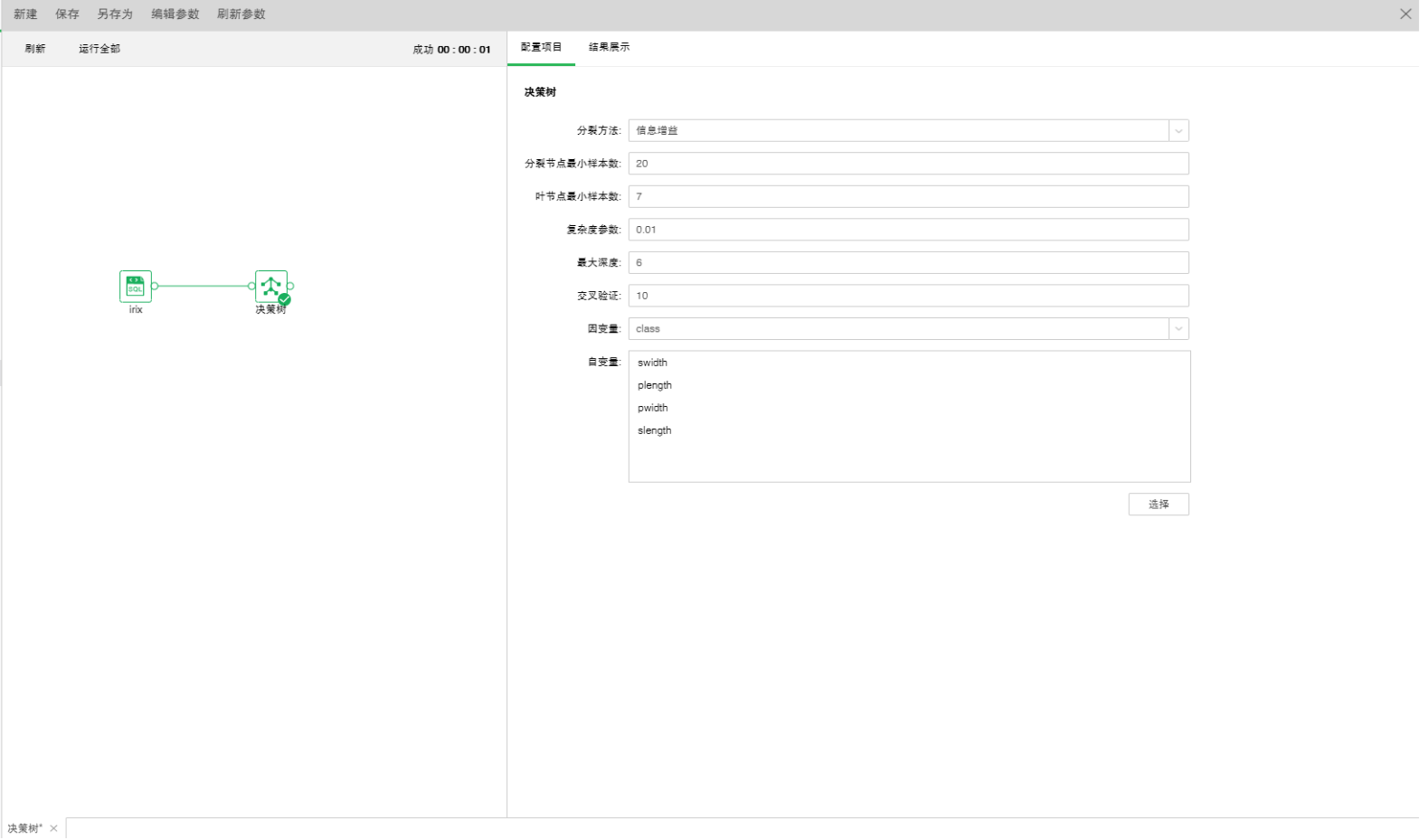
o配置项目
【分裂方法】包含信息增益和Gini系数。
信息增益:划分前后,子集纯度的提升值。
Gini系数:在样本集合中一个随机选中的样本被分错的概率。
【分裂节点最小样本数】样本数小于该值该节点将不进行分裂。默认值20。
【叶节点最小样本数】样本数小于该值,该分支将被剪除。默认值7。
【复杂度参数】每次分裂会计算一个复杂度,当复杂度大于该参数值不再进行分裂。默认值0.01。
【最大深度】决策树的最层次数。默认值6。
【交叉验证】通过交叉验证可以得到最优的方程。默认值是10。
【因变量】从下拉列表中选出需要作为因变量的字段。任何一个系统(或模型)都是由各种变量构成的,当我们分析这些系统(或模型)时,可以选择研究其中一些变量对另一些变量的影响,那么我们选择的这些变量就称为自变量,而被影响的量就被称为因变量。
【自变量】从选择列对话框中选出需要作为自变量的字段。
o结果展示
1. 树形结果
分类结果有两种,二分类和多分类。当因变量只有两个不同值时是二分类;当因变量有多于两个不同值时是多分类。节点最上方是节点编号。节点内有两行,第一行是该节点最终分类;当为多分类时第二行是该节点各种分类的概率值,当为二分类时第二行是该节点是主分类的概率值。yes和no代表是否满足条件,来确定分支方向。节点颜色代表纯度。
二分类树形结果展示如下:
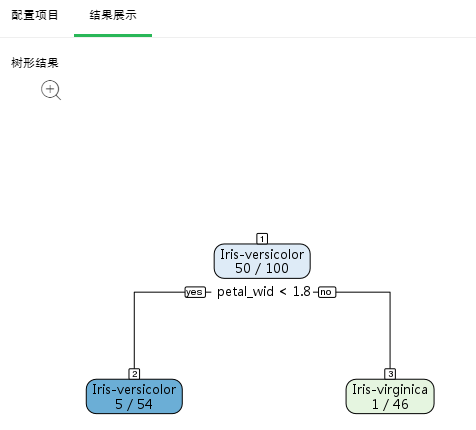
注意: 主分类是绿色节点,蓝色节点的5/54表示Iris-versicolor是Iris-virginica的概率值。
多分类树形结果展示如下:
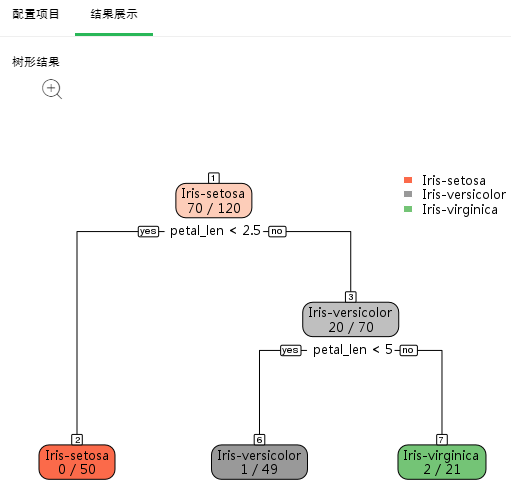
点击放大按钮,可放大图片以更清晰的查看图片。
2. 节点分类情况
列出所有叶子节点的信息。
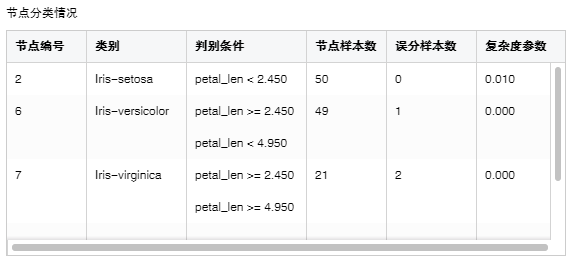
【节点编号】叶子节点的编号。
【类别】叶子节点的类别。
【判别条件】从根部到该叶子节点的判别条件。
【节点样本数】叶子节点的样本数。
【误分样本数】错误分类的样本数。
【复杂度参数】每个叶子节点的复杂度参数。
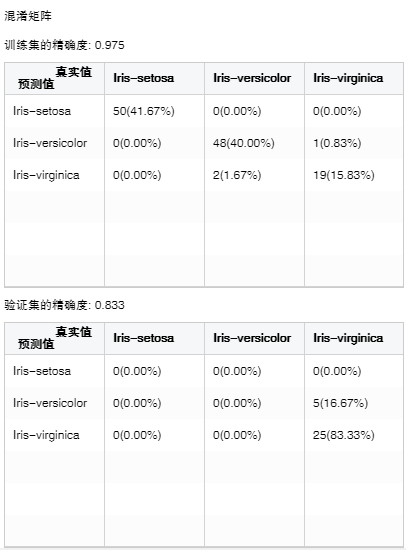
3. 混淆矩阵
预测结果的情形分析表,当有数据分区时还可查看验证集的分析表。
横向表头是真实值,纵向表头是预测值。整数值代表样本个数,百分数是样本个数占总样本个数的比例。精确度为真实值和预测值相同的比例总和。
❖K-Means聚类
K-Means是聚类算法中的一种,其中K表示类别数,Means表示均值。顾名思义K-Means是一种通过均值对数据点进行聚类的算法。K-Means算法通过预先设定的K值及每个类别的初始质心对相似的数据点进行划分,并通过划分后的均值迭代优化获得最优的聚类结果。
为了提升K-Means聚类的计算效率,产品支持分布式系统计算K-Means。当输入节点数据集是“数据集市数据集”时就是分布式计算的。
拖拽一个数据集和一个K-Means聚类节点到编辑区,连接数据集和K-Means聚类节点。选中K-Means聚类节点设置及展示区包含两个页面:配置项目、结果展示。

o配置项目
【训练模式】包含质心数、质心数范围。
【质心数】质心的个数。
【质心数范围】质心个数的范围。
【初始化质心】初始化质心的方法包括:随机距离、Kmeans++。随机距离是所有质心都是随机选取的。Kmean++是第一个质心是随机选取,其它质心按距离选取,距离其它质心越远被选中的概率越大。
【随机数种子】生成随机数的种子。默认值是0。
【距离计算方法】包括两张方法:欧式距离、余弦距离。欧式距离是两个数据点的实际距离。余弦距离是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小的度量。
【最大迭代次数】迭代计算的最大次数,最终算出稳定的质心数。默认值100。
【缺失值填充】用自变量列平均值填充此列的空值。默认是填充的。
【标准化】对自变量标准化,默认标准化方式是Z-Score标准化。
【自变量】从选择列对话框中选出需要作为自变量的字段。
o结果展示
质心数为6,样本个数150,K-Means聚类展示结果如下:
1. 簇分布图
簇内的样本个数占总样本个数的比例。
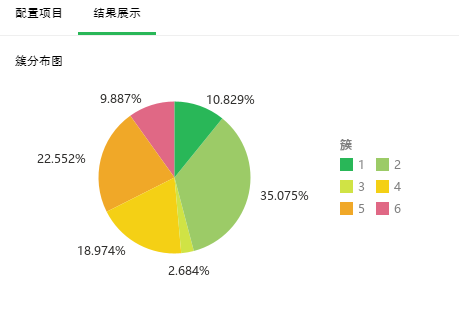
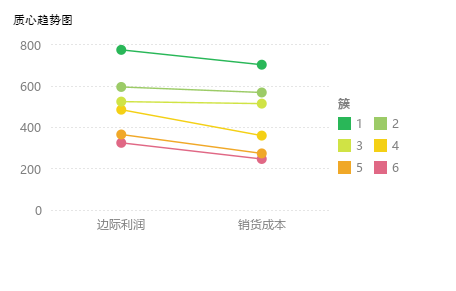
2. 质心趋势图
各个质心在自变量上的变化趋势。
3. 聚类数据展现结果
根据前两个列绘制的聚类之后的散点图。
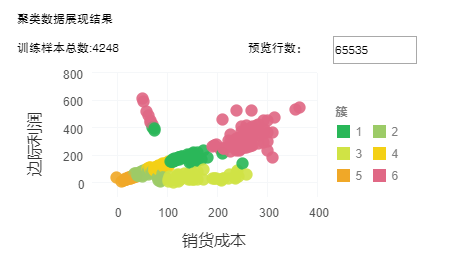
【预览行数】图表默认展示65535行数据,可修改此值改变预览行数。
4. k均值聚类质心
质心在自变量上的取值。
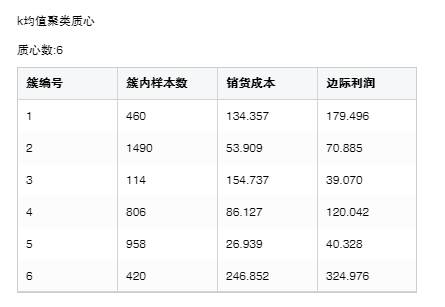
5. 簇成员
样本分别属于哪个簇,距离质心的距离。
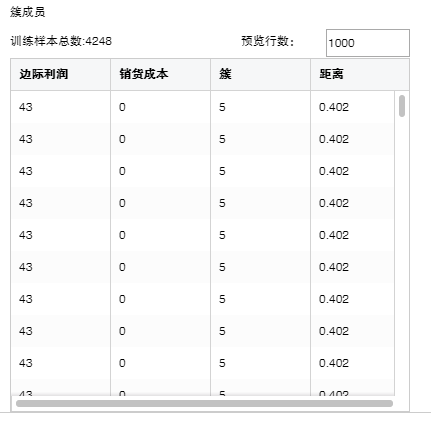
【预览行数】默认预览行数是1000,可修改预览行数。
【簇】分类编号。
【距离】不同距离计算方法计算出的每条样本到最近质心的距离值。
❖关联规则
关联规则(Association Rules)是无监督的机器学习方法,从数据背后发现事物之间可能存在的关联或者联系,用于知识发现,而非预测。这种事物之间的关联或者联系就叫规则。
拖拽一个数据集和一个关联规则节点到编辑区,连接数据集和关联规则节点。选中关联规则节点设置及展示区包含两个页面:配置项目、结果展示。
关联规则包含两种算法:一种为分布式的FG-Growth,另一种为非分布式的Apriori。
oApriori算法
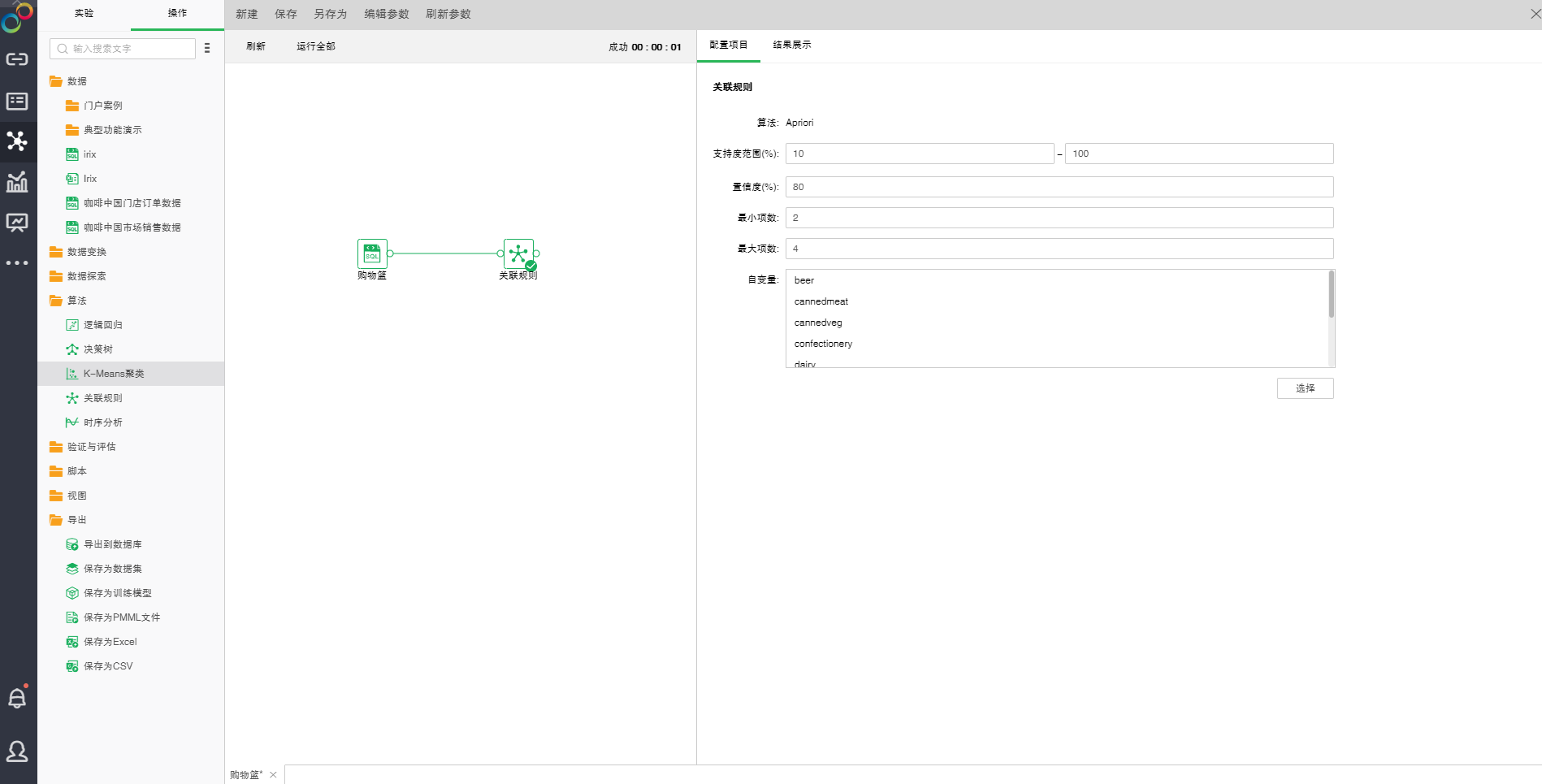
oApriori配置项目
添加关联规则模型到实验后,可通过右侧的“配置项目”页面,对模型进行设置。
【支持度范围(%)】模型所生成的规则的支持度级别的百分比值范围。如果不在此范围内规则将被废弃。
【置信度(%)】模型所生成的规则的置信度级别的最小百分比值。如果模型所生成的规则的置信度级别小于此数量,那么该规则将被废弃。
【最小项数】模型所生成的规则的最小项数,小于此值将被废弃。
【最大项数】模型所生成的规则的最大项数,大于此值将被废弃。
【自变量】从选择列对话框中选出需要作为自变量的字段。
oApriori结果展示
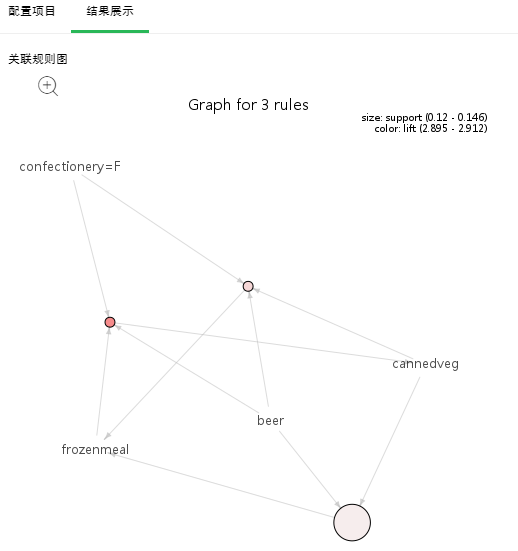
1. 关联规则图
各项的关联关系图,每个圆圈代表一条规则,指向圆圈的是左项,圆圈指向的是右项;圆圈大小代表支持度大小,圆圈越大支持度越大,圆圈颜色代表提升度,颜色越深提升度越大。
点击放大按钮,可放大图片以更清晰的查看图片。
2. 关联规则
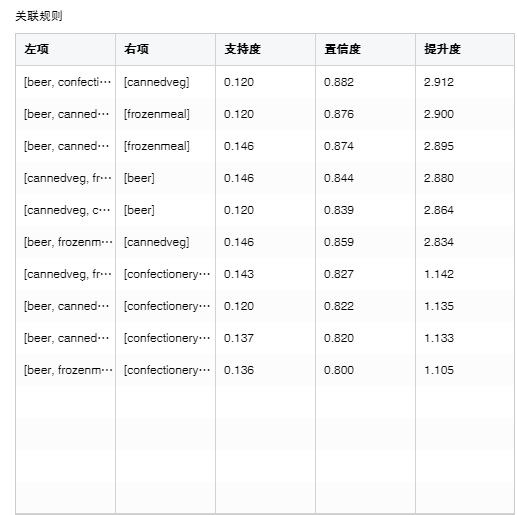
【左项】规则的先导项集。
【右项】规则的结论项集。
【支持度】项集出现的次数除以总的记录数。
【置信度】项集{X,Y}同时出现的次数占项集{X}出现次数的比例。
【提升度】度量项集{X}和项集{Y}的独立性。数值越大模型越好。
oFG-Growth算法
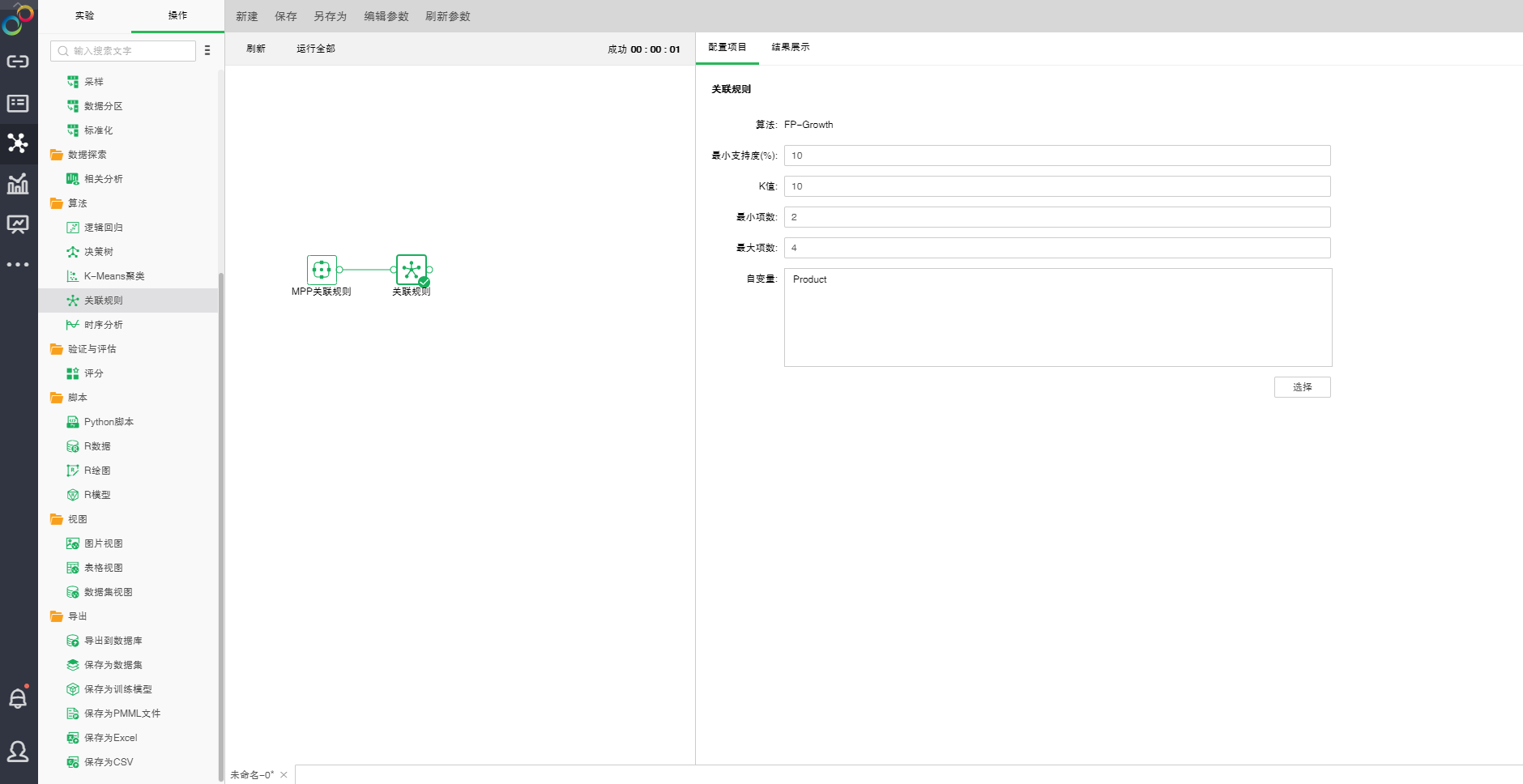
oFG-Growth算法的配置
添加关联规则模型到实验后,可通过右侧的“配置项目”页面,对模型进行设置。
【最小支持度(%)】最小支持度用来度量一个集合在原始数据中出现的频率。如果不在此范围内规则将被废弃。
【K值】模型所生成的项目展示的行数。
【最小项数】控制频繁项集的最小长度,小于此值将被废弃。
【最大项数】控制频繁项集的的最大长度,大于此值将被废弃。
【自变量】从选择列对话框中选出需要作为自变量的字段。
oFG-Growth结果展示
关联规则模型运行成功后,可通过右侧的“结果展示”页面,查看实验模型的结果。
1.关联规则
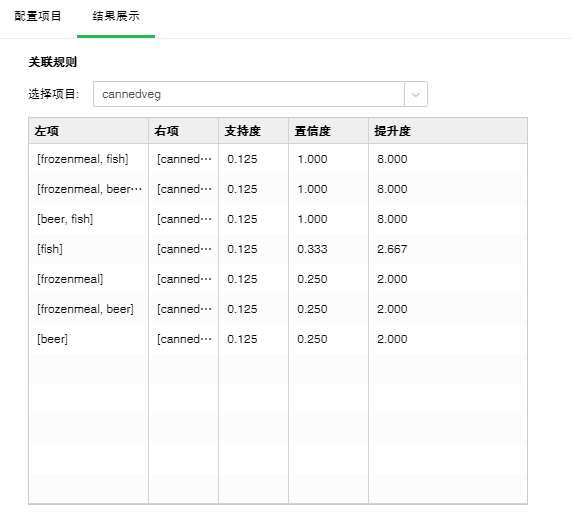
【选择项目】数据库中的字段所包含的其中一个项目。
【左项】规则的先导项集。
【右项】规则的结论项集。
【支持度】项集出现的次数除以总的记录数。
【置信度】项集{X,Y}同时出现的次数占项集{X}出现次数的比例。
【提升度】度量项集{X}和项集{Y}的独立性。数值越大模型越好。
❖时序分析
时序分析通过考虑水平趋势和季节性趋势,对一段时间内、等时间间隔的采样数据进行分析,以预测未来一段时间的数据。即根据已知的历史数据,预测未来的数据。
拖拽一个数据集和一个时序分析节点到编辑区,连接数据集和时序分析节点。选中时序分析节点设置及展示区包含两个页面:配置项目、结果展示。
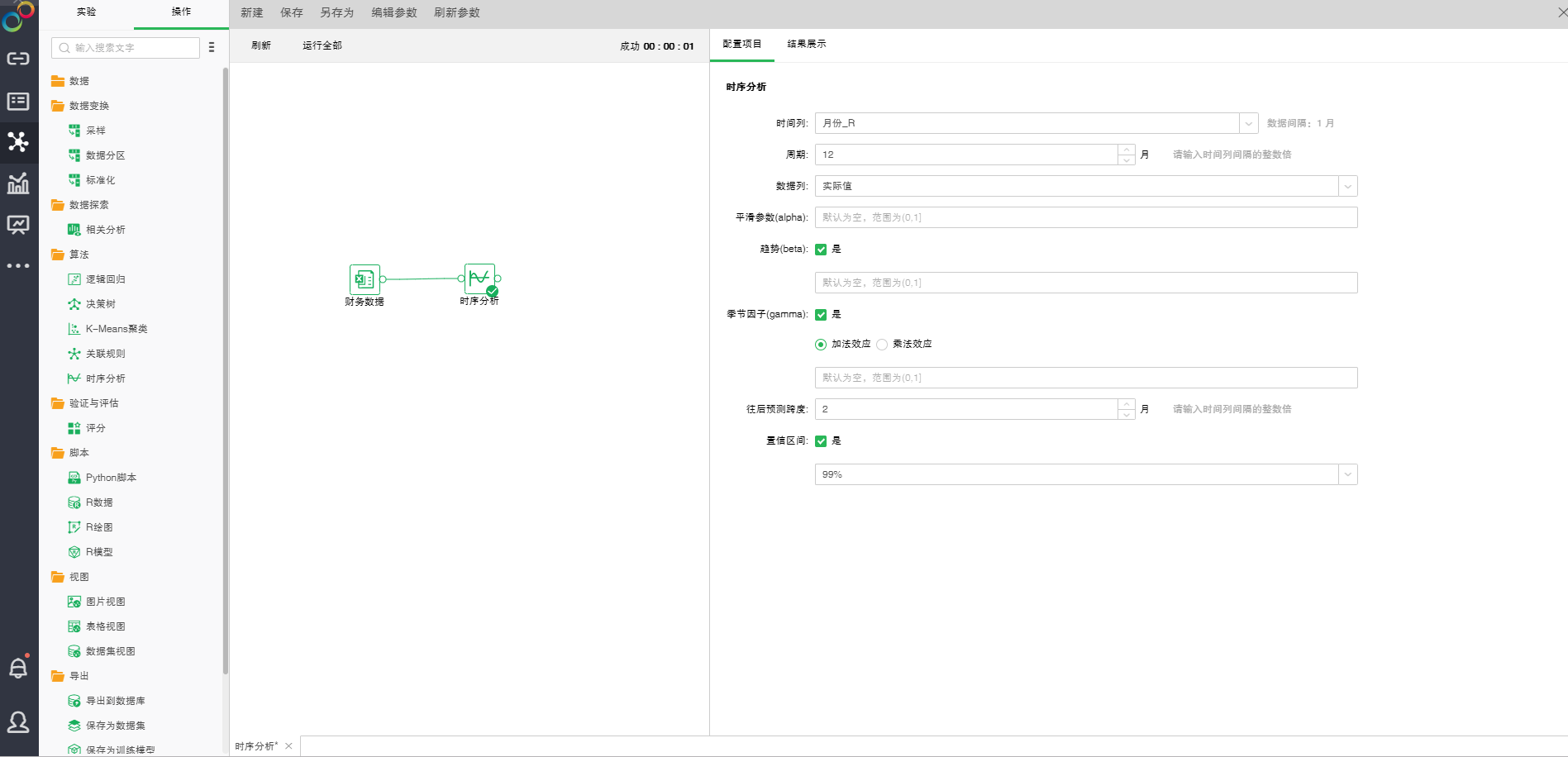
o配置项目
【时间列】选择时间字段。根据选择的时间字段的数据,自动算出时间间隔。
【周期】需填入时间间隔的整数倍,根据周期和时间间隔(周期/ 时间间隔)算出频率,即单位时间内的观测数。根据时间间隔,系统会自动往周期填入一个合理的数值,此数值也可手动修改。
【数据列】选择数据字段。
【平滑参数(alpha)】α越接近1,平滑后的值越接近当前时间的数据值。
【趋势(beta)】是否考虑纵向趋势。默认是被勾选,表示按纵向趋势拟合。
【季节因子(gamma)】是否考虑季节性趋势。如果设置为不勾选(FALSE),则非季节性模型拟合。如果设置为勾选,则进行季节性模型拟合。季节性模式可以是加法效应(additive)和乘法效应(multiplicative)。加法效应默认勾选,表示按季节性加法的趋势增长。乘法效应被勾选时,表示按季节性乘法趋势增长。季节性模型拟合时,需满足一个周期内至少有两个数据点,即频率大于等于2,且时间序列至少包含2 个周期。
【往后预测跨度】往后预测的时间跨度,需填入时间间隔的整数倍。选择时间列后,系统会自动填入一个合理的数值,此数值也可进行手动修改。
【置信区间】根据Level 算出估计值的上界和下界,默认Level 是99%。
o结果展示
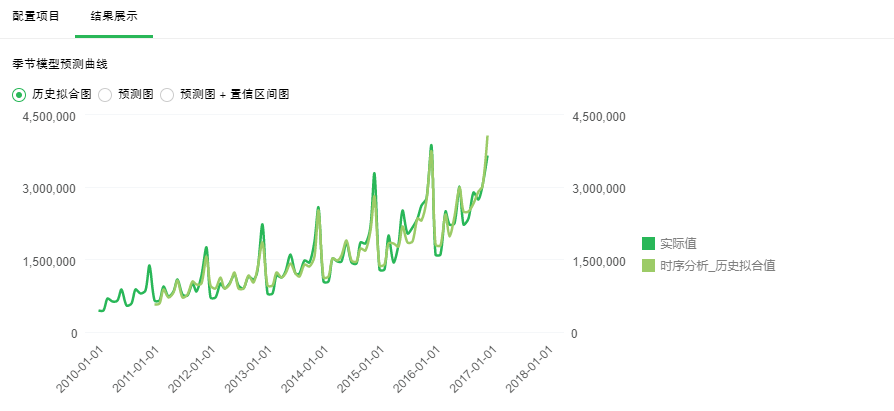
1. 季节模型预测曲线
【历史拟合图】历史数据变化曲线和拟合数据变化曲线。深绿色线是历史数据变化曲线,浅绿色线是拟合数据变化曲线。两条线重合度越高拟合的越好。
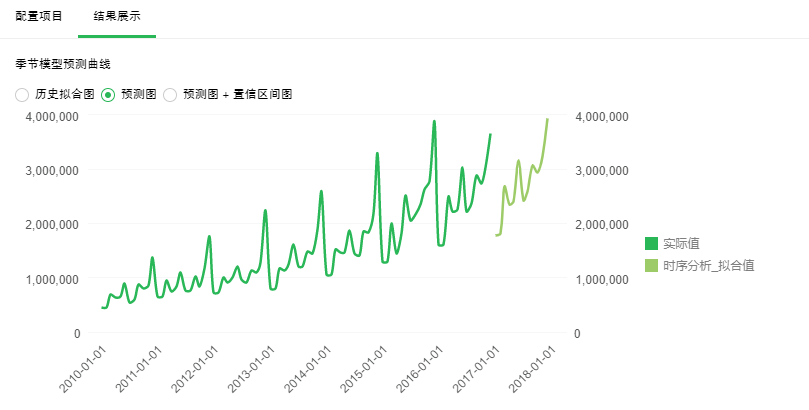
【预测图】对未来指定时间段内的预测。深绿色线是历史数据变化曲线,浅绿色线是对指定时间段内预测的变化曲线。由此可以看出未来数据的变化趋势。
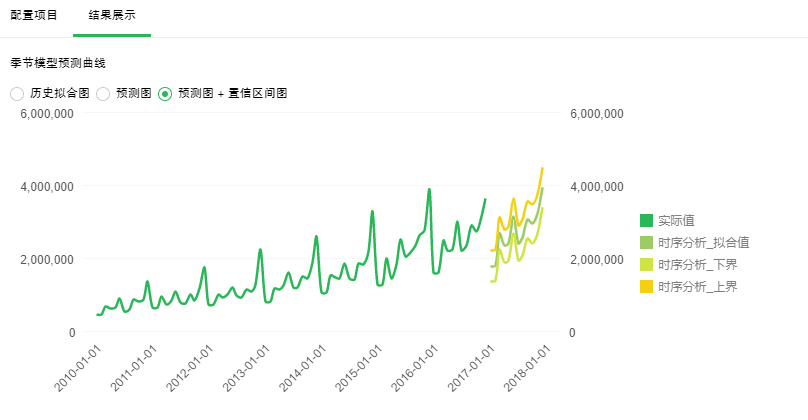
【预测图+置信区间图】对未来指定时间段内的预测。深绿色线是历史数据变化曲线,浅绿线指定时间段内预测的变化曲线。黄色线是置信区间的上界,橙色线是置信区间的下界。
2. 模型统计量
【MSE】平方误差的均值。越小越好。
【LBQ检验】时间序列是否存在滞后相关的一种统计检验。显著性小于0.05时说明误差存在明显的自相关性,表示模型拟合不良。显著性值越接近1模型拟合越好。